Student Perspective: Exploring Quantum Fluctuations with Twesh Upadhyaya

This story is part of our new Student Perspective series to showcase student voices in RQS research. The following article is by Twesh Upadhyaya, a physics doctoral student and member of the RQS Student-Postdoc Council.

Can heat flow from hot to cold? Can errors in error correction itself be fixed? And what does all of this have to do with cars? Read on to find out! 

Quantum systems are easily disturbed by their environment. This renders them prone to stochastic fluctuations. These fluctuations can wreak havoc if they are not characterized and mitigated. Consider an analogy: Suppose you walk into a car dealership and the salesman offers you a car with a new type of engine. “It averages 30 miles per gallon,” he says. “Great,” you think to yourself. “But,” he continues, “the performance can fluctuate significantly around this average. Sometimes you’ll get 40 MPG and sometimes only 10.” Now you’re not so sure about this car. You won’t be able to predict its fluctuations, so what will you do if you’re on a long drive with gas stations few and far between?

In other words, it isn’t just the average performance of a device which is important; understanding the fluctuations in behavior is equally crucial. Large, classical systems like car engines typically exhibit small deviations in performance, so we don’t often worry about this variation in our day-to-day lives. But for quantum systems, the situation is far different. Quantum systems are typically small and delicate and difficult to insulate from their noisy environment. And even in a noiseless experimental apparatus, measurement introduces unavoidable randomness. 

Researchers at the RQS are developing novel techniques to manage and mitigate these fluctuations for quantum systems. Here we highlight three recent results from the Institute, covering both theoretical and experimental work. These lines of research fall into two categories. The first is improving the practical performance of quantum simulators by characterizing and mitigating the noise they experience from the environment. This can be accomplished by carefully tailoring the environment to reduce harmful noise-reservoir engineering—or by increasing the robustness of the quantum systems through redundancy—error correction. The second is understanding the fundamental properties of fluctuations in quantum systems and the resultant entropy production.

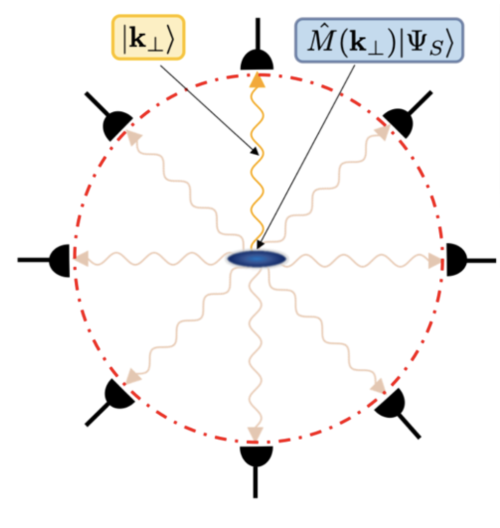
One way in which fluctuations can arise is when a system interacts with an environment. Thus, controlling the evolution of the environment can induce control of the system. In a recent publication, Emine Altuntaş and Ian Spielman examine how a tuned environment changes the evolution of a quantum system [1]. Specifically, the authors consider a Bose-Einstein condensate interacting with a laser beam. The photon density in the reservoir is periodically measured by the environment. This can be modeled by a set of photodetectors surrounding the trap. The location of the triggered detector indicates the direction the photon was traveling in (see Figure 1). By varying the measurement strength—experimentally via the detuning and modeled theoretically by the rate of the detection measurements—the authors demonstrate experimental control over the Ramsey contrast. The Ramsey contrast, obtained through interferometry, encodes information about the state of the quantum system. Hence, the authors demonstrate control over the quantum state by tuning its interactions with the environment.

Image

Even when the environment cannot be controlled, researchers at the RQS are finding new ways to protect quantum simulators from noise, using quantum error-correcting codes. These codes use extra qubits to redundantly encode information. Errors on a single one of the qubits can then be detected and corrected. However, even these measurements are subject to fluctuations! Hence, it is useful to have codes which work even if there are errors in the measurements themselves; they are known as single-shot codes. In recent work [2], Yingjia Lin, Shilin Huang, and Ken Brown construct single-shot check measurements for the toric code, a popular quantum error-correcting code. The authors start with the conventional check measurements for the toric code and then stitch them together to create the single-shot measurements, using Gaussian elimination to avoid redundancies. Unfortunately there is a price to pay for this improved performance—the new check measurements are not all local; some are stretched out across the torus of qubits (see Figure 2). This can make them more challenging to implement.

Image

The authors perform simulations to demonstrate that their codes are more robust to errors than the conventional ones when measurements are noisy. They also consider a different error simulation where the probability of an error increases with the weight of the stabilizers, i.e. the number of qubits on which the check measurement is performed. In this case, they find that conventional check measurements actually perform better. This highlights the importance of characterizing fluctuations accurately when designing quantum devices.

Fluctuations can lead to counterintuitive phenomena in fundamental physics. Consider an experiment in which a hot and cold system are brought together for a fixed amount of time. Over many repetitions of such an experiment, energy flows on average from hot to cold, generating entropy. However, the heat flow in any given trial of such an experiment is variable—fluctuations can even lead to heat sometimes flowing from the cold system to the hot one! While these fluctuations are well-understood for classical systems and restricted classes of quantum systems, in [3], Twesh Upadhyaya, Billy Braasch, Gabriel Landi, and Nicole Yunger Halpern investigate the fluctuations for more general quantum systems.

A fundamental tenet of quantum mechanics is the existence of observables which cannot be measured simultaneously; for example, the spin of an atomic nucleus in the X, Y, and Z directions. Consider a variation on the above heat-flow experiment: two atoms exchange atomic spin components, such that the total spin is conserved but the spin is transported between the two atoms. As before, the transport is stochastic, the amount of spin exchanged will fluctuate over different trials, and the spin flow will generate entropy. Unlike the case of energy, trying to measure, say, the Z spin component will disturb the flow of the other components. Hence, studying these spin currents requires new tools. 

The authors use weak measurements to address the quantum systems without disturbing them too much. The measurement outcomes are naturally described by quasiprobabilities, a generalization of probabilities that model classical systems.

The authors show that three different definitions of the entropy production, which are normally equivalent, become inequivalent due to noncommutation—the inability to simultaneously measure different components of the flowing currents. One of the entropy definitions can have an imaginary component. This imaginary component signals contextuality, a precise form of nonclassicality, in an experiment where, say, Z-spin is measured before and after the two atoms interact. Analogous to classical systems, the entropy production arises from an irreversibility of the paths the quantum system takes through state space.

Fluctuations abound in the natural world and are inherently present in quantum systems. Researchers at the RQS are making progress in understanding the fundamental nature of these fluctuations, how to protect quantum devices against these fluctuations, and how to tune these fluctuations to be useful.

REFERENCES

[1] E. Altuntaş, I.B. Spielman, Quantum back-action limits in dispersively measured Bose-Einstein condensates. Commun Phys 6, 66 (2023).

[2] Y. Lin, S. Huang, K. R. Brown, Single-shot error correction on toric codes with high-weight stabilizers. Phys. Rev. A 109, 052438 (2024).

[3] T. Upadhyaya, W.F. Braasch, Jr., G.T. Landi, N. Yunger Halpern, Non-Abelian Transport Distinguishes Three Usually Equivalent Notions of Entropy Production. PRX Quantum 5, 030355 (2024).